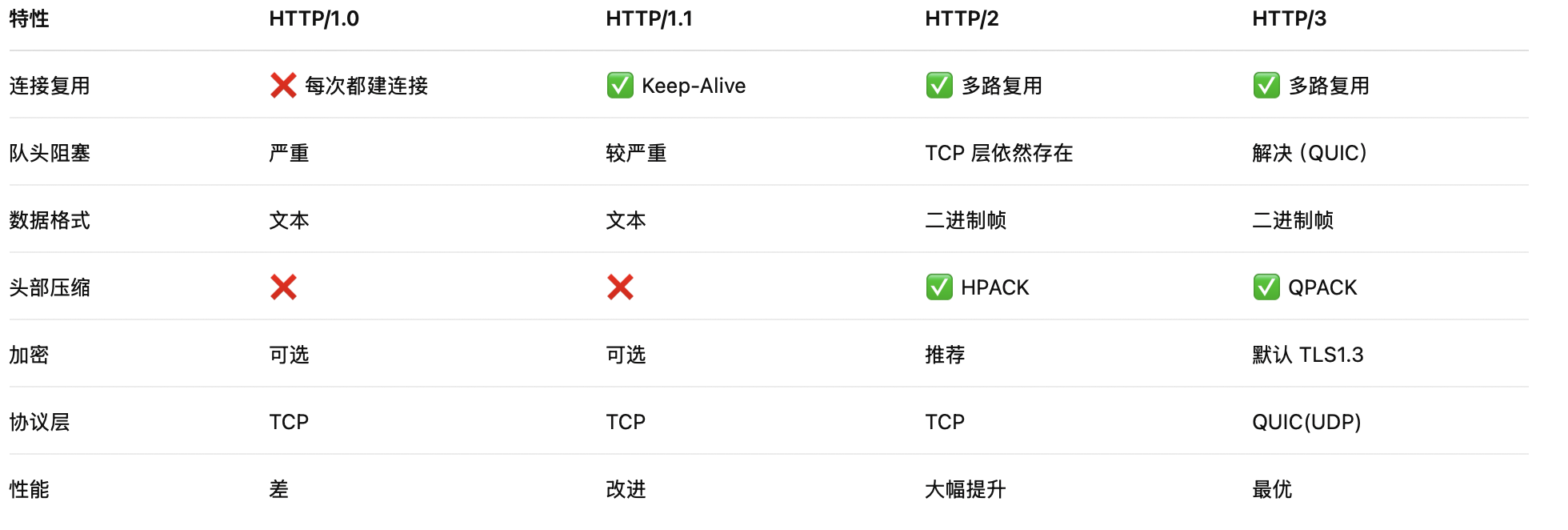
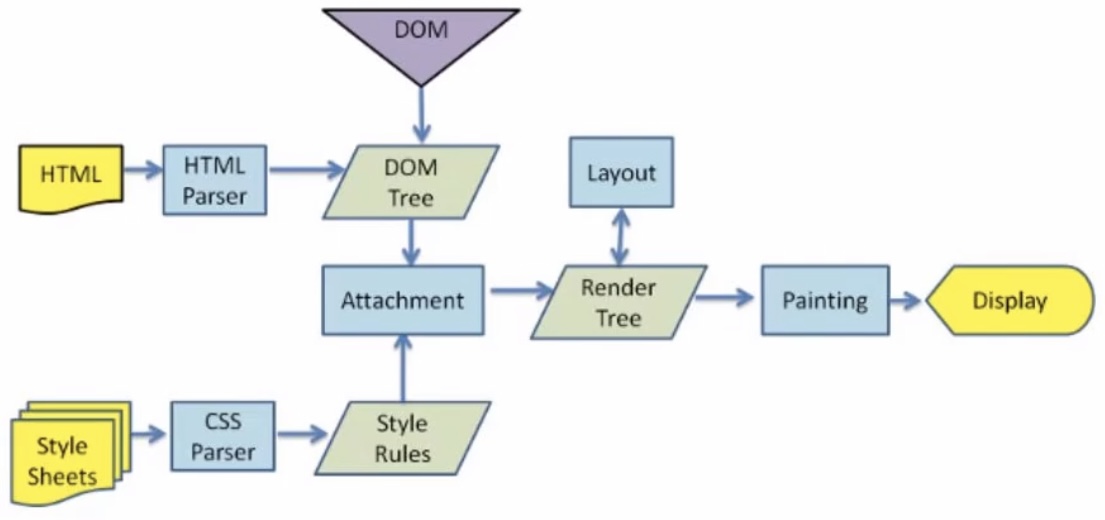
推荐系统架构
推荐和搜索的核心任务是从海量物品中找到用户感兴趣的内容。
系统架构
一般推荐系统架构分为离线层(Offline)、近线层(Nearline)和在线层(Online)。
- 离线层:不实用实时数据,不提供实时响应。
- 数据处理、数据存储。
- 特征工程、离线特征计算。
- 离线模型训练。
- 优势与不足:数据量级最大,需要存储海量数据、大规模特征工程以及多机分布式模型训练。当前主流通过HDFS收集业务数据,通过Hive等大数据工具进行数据提取、筛选以及处理。主流框架是Spark。可以进行批量处理与计算而没有响应时间的要求。
- 近线层:使用实时数据,不保证实时响应。
- 不严格要求实时性,但需要弥补离线层与在线层之间的不足。适合处理对时延较为敏感的任务。
- 特征的事实更新计算:离线层数据与实时数据分布不一致,通过近线层调节。
- 获取实时训练数据:用户较短时间内产生的数据特征可以通过近线层直接输入模型。
- 模型实时训练:通过在线学习的方法更新推送模型。
- 主流大数据框架:Flink,Storm。
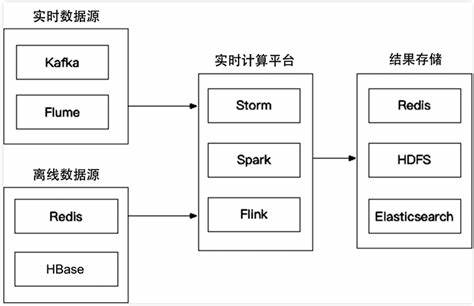
- 不严格要求实时性,但需要弥补离线层与在线层之间的不足。适合处理对时延较为敏感的任务。
- 在线层:使用实时数据,保证实时在线服务。
- 面向用户的一层,对响应时延有要求,需要立即响应推荐结果。
- 模型在线服务:包括了快速召回和排序。
- 在线特征快速处理拼接:根据传入的用户ID和场景,快速读取特征和处理。
- AB实验或分流:根据不同用户采用不一样的模型,比如冷启动用户和正常服务模型。
- 运筹优化和业务干预:比如对特殊商家的流量扶持、对特定内容的限流。
- 面向用户的一层,对响应时延有要求,需要立即响应推荐结果。
算法架构
推荐系统会细分为四个阶段:召回、粗排、精排、重排.
- 召回:从推荐池中选取大量items送个后续排序模块。
- 由于面对的候选集庞大且需要在线输出,所以召回模块需要轻量快速低延迟。不需要十分准确,但不可遗漏。
- 考虑内容:
- 用户层面:用户需求、兴趣与场景多元化。
- 系统层面:增强鲁棒性。兜底。
- 多样性内容分发:召回目标多元。
- 可解释性。
- 粗排:对召回结果进行初步筛选送给精排。兼顾准确性和低延迟。
- 考虑内容:
- 根据精排模型的重要特征来做候选集的截断。
- 根据与user相关性进行召回结果截断。
- 性能保证。
- 考虑内容:
- 精排:大部分算法研究的层面。对粗排的候选集进行打分和排序。
- 重排:解决精排结果可能同质化和冗余的问题。以及根据运营策略等去影响精排结果。是对精排结果的微调。
技术栈
画像层
推荐系统的物料库,绘制用户、商品画像等。通过tag的方式进行统计。
- 内容特征提取与标签分类
- 文本理解:RNN,TextCNN,FastText,Bert等。
- 关键词标签:TF-IDF,Bert,LSTM-CRF。
- 内容理解:TSN,RetinaFace,PSENet等。
- 知识图谱:KGAT,RippleNet。
召回/粗排
经典模型召回:FM,双塔DSSM,Multi-View DNN等。 序列模型召回:CBOW,Skip-Gram,GRU,Bert等。 用户序列拆分:对用户的多维兴趣进行拆分,刻画更细致的方向。 知识图谱:对推荐结果的可解释性。 图模型:通过图模型来表示系统。
精排
研究最多的方向,主要通过各种深度学习方法进行打分排序。