Cousins in Binary Tree II

Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins’ value. Two nodes of a binary tree are cousins if they have the same depth with different parents. Return the root of the modified tree.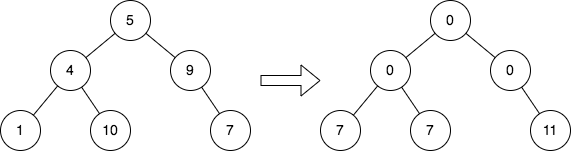

Examples:

Input: root = [5, 4, 9, 1, 10, null, 7];
Output: [0, 0, 0, 7, 7, null, 11];

Input: root = [3, 1, 2];
Output = [0, 0, 0]

Constraints:

• The number of nodes in the tree is in the range [1, 10⁶].
• 1 ≤ Node.val ≤ 10⁴

Solution

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    TreeNode* replaceValueInTree(TreeNode* root) {
        if (!root) return nullptr;
        queue<TreeNode*> q;

        int prev = root->val;
        q.push(root);

        while (!q.empty()) {
            int n = q.size();
            int curr = 0;
            while (n--) {
                TreeNode* temp = q.front();
                q.pop();
                int childrenSum = (temp->left ? temp->left->val : 0) + (temp->right ? temp->right->val : 0);

                if (temp->left) {
                    temp->left->val = childrenSum;
                    q.push(temp->right);
                }
                if (temp->right) {
                    temp->right->val = childrenSum;
                    q.push(temp->right);
                }

                curr += childrenSum;
                temp->val = prev - temp->val;
            }
            prev = curr;
        }
        return root;
    }
}

Explanation: The whole process of this solution is based on the breadth-first traversal of a binary tree. We use variable n to hold the remained elements in the queue. Then calculate the sum of the children nodes of the front-element in the queue then pop it after finishing the computation. Then push all children nodes of current node into the queue if it has. At first, we use current node to hold the sum of its siblings and itself, and use variable prev to hold the sum of nodes in the same level. Then subtract the prev with itself can get the sum of its cousins. In short, the logic of this solution is to calculate the sum of children nodes of current node and store the sum into the all of its children nodes (which are siblings for each other). And calculate the sum of the whole level, then subtract the sum by each node’s value (which is the sum of itself with its sibling) can get the sum of cousins. If there is only two nodes in a level, each nodes get no cousins, thus the sum of whole level equals the sum with sibling, hence the result that store into this node is zero.