Blog | Autzoko Lang

春寒歲裏鴻都郎，憑誰望，海客鄉。乞聞風中烟花聲。牖鼓雲浪，孤看飛航，一日夜光藏。 山外山隔窗外窗，凍雪殘餘鬢頭霜。玉樓歌裏獨醉好。一曲彷徨，不奏迷惘，笑寫清平殤。

天山大漠越東海，蒼黃故土，清霾掩我故城。 不望天山萬仞，東方一點紅，半載西風吹不動，車馬喧囂，醉雲西沈。 猶見酒綠燈紅処，大千世界任我行。 惟問世間何方進，天海相隔步難停。 慾走萬里尋真切，怎理身後多少名。 進退不知馮唐夢，稼軒詞外難堪情。 西門外，游人慶，渡走灞橋心難盈。 撩落枝亂十二載，是非成敗幾回明。 蒼茫連天撲塵土，天河兩岸信難聆。 白日清夢誰人語，魚游池塘畫新屏。

風殘蓬柳斜波碧，餘暉催月移星洛。 懷客凴西堤，西霞映相依。 湖光朱燈染，浮華隱河漢。 此夜棲君夢，醉與君相擁。

巷下新春卻回避，靜雪猶嘯北風欺。 京城死地無涯処，青首難吟摩詰詩。

秋風渡裏，長望雲烟點鄉愁。 亭雨空，落花怎得來相守，難回首。 待到思憶悄悄話朦朧，一片故園夢，晚風意正濃。 催我相思萬般，不憶北風，不憶秋冬。 何時踏足何時了，瀟瀟琴語，瀟瀟風雨。

You are given an integer n indicating there are n specialty retail stores. There are m product types varying amounts, which are given as a 0-indexed integer array quantities, where quantities[i] represents the number of products of the i^th product type. You need to distribute all product to the retail stores following these rules:

• A store can only be given at most one product type but can given any amount of it.
• After distribution, each store will have been given some number of products (possibly 0), Let x represent the maximum number of products given to any store. You want x to be as small as possible, i.e., you want to minimize the maximum of products that are given to any store.

Return the minimum possible x.

Example:

1
2
3

Input: n = 6, quantities = [11, 6];
Output = 3;
The 11 products of type 0 are distributed to the first four stores in the amount of [2, 3, 3, 3]. The 6 products of type 1 are distributed to the other two stores in the amount of [3, 3].

1
2
3

Input: n = 7, quantities = [15, 10, 10];
Output: 5;
[5, 5, 5, 5, 5, 5, 5];

1
2

Input: n = 1, quantities = [10000];
Output = 10000;

Constraints:

• 1 ≤ m ≤ n ≤ 10⁵
• 1 ≤ quantities_i ≤ 10⁵

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution {
public:
    int minimizedMaximum(int n, vector<int>& quantities) {
        int low{1}; // same as 'int low = 1;', but in a more safe way.
        int high = *max_element(quantities.begin(), quantities.end());
        while (low < high) {
            int mid = (low + high) / 2;
            int needed{0};
            for (int q : quantities) {
                needed += (q + mid - 1) / mid;
            }
            if (needed <= n) high = mid;
            else low = mid + 1;
        }
        return low
    }
}

Explanation: The key idea of this solution is binary search, the variable mid here is used to indicate the possible maximum quantity that can be distributed to a single store. Variables low and high hold the lower bound and the upper bound of the quantity for distribution. Then use binary search to update the variable mid to find the possible minimized maximum quantity. The way to update mid is to check whether this value can be distributed within n stores. Here using variable needed to hold the number of store that needs for distributing under mid. So traverse the quantities to compute the needed number of stores to distribute q products under mid is the upper bound. For example, if q=7 then mid=3, since 7 products need 3 stores. If needed is less than n, which means the value of mid is greater, and there might a smaller solution, thus update high with mid. Otherwise, mid is to small, thus update low with mid + 1. When low and high converge, which means the minimized value mid is found, then return low.

You are given a 0-indexed array of positive integers nums. In one operation, you can swap any two adjacent elements if they have the same number of set bits (1 presented in binary). You are allowed to do this operation any number of times (including zero). Return true if you can sort the array, else return false.

Examples:

1
2

Input: nums = [8, 4, 2, 30, 15] => [0x1000, 0x100, 0x10, 0x11110, 0x1111];
Output: True => Sorted to [0x10, 0x100, 0x1000, 0x1111, 0x11110] == [2, 4, 8, 15, 30];

1
2

Input: nums = [3, 16, 8, 4, 2];
Output: False;

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
public:
    static bool canSortArray(const vector<int>& nums) {
        uint16_t pmax = 0, cmin = 0; cmax = 0;
        uint8_t pcnt = 0;
        for (const uint16_t v : nums) {
            if (const uint8_t ccnt = popcount(v); pcnt == ccnt) {
                cmin = min(cmin, v);
                cmax = max(cmax, v);
            } else if (cmin < pmax) {
                return false;
            } else {
                pmax = cmax;
                cmin = cmax = v;
                pcnt = ccnt;
            }
        }
        return cmin >= pmax;
    }
}

Explanation:

This solution divides the array into several groups by the number of bits that are set. The popcount() function here is an library function that used to find the number of set bits in a variable. And the if (const uint8_t ccnt = popcount(v); pcnt == ccnt) structure is to define a variable within the if-else if-else structure and use it for boolean expression in a brief way. The if-else if-else structure in the code is doing mainly for:

• Checking set bits of current variable v, if current number of set bit ccnt equals the number of set bits of last variable pcnt, then they are in the same group. Then update the maximum and the minimum value of current group into cmin and cmax.
• If the minimum value of current group cmin is less than the greatest value of the last group pmax, then this array cannot be sorted because every number that presents in a relative back group must be greater than every number in a front group. Thus, program return false here.
• If ccnt does not equal pcnt, current value v belongs to a new group, so the maximum value of current group is assigned to pmax, the maximum of the previous group, then update cmin and cmax with current value, and pcnt with the number of set bit of v.

Above all, the core of this solution is to guarantee that for each group, their minimum value must be greater than the maximum value of every group in its front.

Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins’ value. Two nodes of a binary tree are cousins if they have the same depth with different parents. Return the root of the modified tree.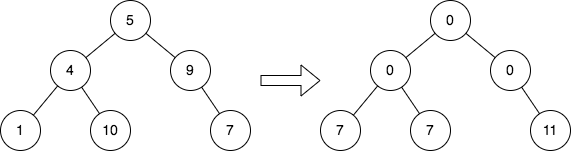

Examples:

1
2

Input: root = [5, 4, 9, 1, 10, null, 7];
Output: [0, 0, 0, 7, 7, null, 11];

1
2

Input: root = [3, 1, 2];
Output = [0, 0, 0]

Constraints:

• The number of nodes in the tree is in the range [1, 10⁶].
• 1 ≤ Node.val ≤ 10⁴

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    TreeNode* replaceValueInTree(TreeNode* root) {
        if (!root) return nullptr;
        queue<TreeNode*> q;

        int prev = root->val;
        q.push(root);

        while (!q.empty()) {
            int n = q.size();
            int curr = 0;
            while (n--) {
                TreeNode* temp = q.front();
                q.pop();
                int childrenSum = (temp->left ? temp->left->val : 0) + (temp->right ? temp->right->val : 0);

                if (temp->left) {
                    temp->left->val = childrenSum;
                    q.push(temp->right);
                }
                if (temp->right) {
                    temp->right->val = childrenSum;
                    q.push(temp->right);
                }

                curr += childrenSum;
                temp->val = prev - temp->val;
            }
            prev = curr;
        }
        return root;
    }
}

Explanation: The whole process of this solution is based on the breadth-first traversal of a binary tree. We use variable n to hold the remained elements in the queue. Then calculate the sum of the children nodes of the front-element in the queue then pop it after finishing the computation. Then push all children nodes of current node into the queue if it has. At first, we use current node to hold the sum of its siblings and itself, and use variable prev to hold the sum of nodes in the same level. Then subtract the prev with itself can get the sum of its cousins. In short, the logic of this solution is to calculate the sum of children nodes of current node and store the sum into the all of its children nodes (which are siblings for each other). And calculate the sum of the whole level, then subtract the sum by each node’s value (which is the sum of itself with its sibling) can get the sum of cousins. If there is only two nodes in a level, each nodes get no cousins, thus the sum of whole level equals the sum with sibling, hence the result that store into this node is zero.

Given the root of a binary tree and a positive integer $ k $. The level sum in the tree is the sum of the values of the nodes that are on the same level. Return the k^th largest level sum in the tree (not necessary distinct). If there are fewer than k levels in the tree, return -1.

Example:

1
2
3

Input: root = [5, 8, 9, 2, 1, 3, 7, 4, 6], k = 2;
Output: 13;
Explanation: Level 3 has the 2nd largest sum;

1
2

Input: root = [1, 2, null, 3], k = 1;
Output: 3;

Constraints:

• The number of nodes in the tree is n.
• 2 ≤ Node.val ≤ 10⁵
• 1 ≤ k ≤ n

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    long long kthLargestLevelSum(TreeNode* root, int k) {
        vector<long long> res;
        queue<TreeNode*> q;

        q.push(root);

        while(!q.empty()) {
            int n = q.size();
            long long sum = 0;

            while (n--) {
                sum += (long long)q.front()->val;
                if (q.front()->left) q.push(q.front()->left);
                if (q.front()->right) q.push(q.front()->right);
                q.pop();
            }
            res.push_back(sum);
        }

        if (k > res.size()) return -1;
        sort(res.begin(), res.end(), greater<long long>());

        return res[k - 1];
    }
};

Explanation: Since this problem needs us to calculate the sum of each level of the binary tree, a breadth-first traversal is required. The most used method for breadth-first traversal is to use a queue, the CPP style example code is this:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

void printTreeBreadthFirst(TreeNode* root) {
    queue<TreeNode*> q;

    if (root != nullptr) {
        q.push(root);
    }

    while (!q.empty()) {
        cout << q.front()->val << " --> ";
        if (q.front()->left) q.push(q.front()->left);
        if (q.front()->right) q.push(q.front()->right);
        q.pop();
    }
}

In this problem, the variable n holds the number of nodes in this level, which n equals current size of the queue. Thus, it only needs to use a inner loop to calculate the sum of the level by popping values from the queue, and meanwhile import the nodes of the next level by accessing the children of current head node of the queue.

Given two 0-indexed integer arrays nums1 and nums2, return a list answer if size 2 where:

• answer[0] is a list of all distinct integers in nums1 which are not present in nums2.
• answer[1] is a list of all distinct integers in nums2 which are not present in nums1.

Examples:

1
2

Input: nums1 = [1, 2, 3], nums2 = [2, 4, 6];
Output = [[1, 3], [4, 6]];

1
2

Input: nums1 = [1, 2, 3, 3], nums2 = [1, 1, 2, 2];
Output: [[3], []];

Constraints:

• 1 ≤ len(nums1), len(nums2) ≤ 1000
• −1000 ≤ nums1_i, nums2_i ≤ 1000

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

class Solution {
public:
    vector<vector<int>> findDifference(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> set1(nums1.begin(), nums1.begin());
        unordered_set<int> set2(nums2.begin(), nums2.begin());

        vector<int> distinct_nums1, distinct_nums2;

        for (int num : set1) {
            if (set2.count(num) == 0) distinct_nums1.push_back(num);
        }
        for (int num : set2) {
            if (set1.count(num) == 0) distinct_nums2.push_back(num);
        }

        return {distinct_nums1, distinct_nums2};
    }
}

Explanation:

Convert the two array into set, same elements will be merged within a set, and since the unordered_set in C++ is implmented with hash table with separate chaining method, using a specific algorithm to hash element into difference bucket which points to a chain that contains valid elements. Thus, in ideal case, the find function can get the target value with the time complexity of O(1), and the worst case the time complexity reduces to O(n). So, in the solution, the unordered_set is utilized to merge same elements and for faster method to judge whether a value the set is contained.